Oyunları çözmek için uygun teknikleri geliştirmede kullanılacak iki temel önerme (teorem) vardır:

Önerme 1
M satır ve n sütunu gösterirse (mxn) bir dikdörtgen oyunudur. Her dikdörtgenin bir oyun değeri vardır. Dikdörtgen oyunda herhangi bir oyuncunun her zaman optimal stratejisi vardır. Bu, şöyle ifadelendirilir:

B.D.(x*,y*)=v

Burada minimax ve maximin kuralları uygulanır.

Önerme 2
Herhangi bir dikdörtgen oyunda A ve B oyuncuları için oyunun değeri v, optimal strateji vektörleri de x*,y* olsun.
a)  A oyuncusunun her tam strateji vektörü xt için B.D.( xt, y*) ≤v dir. Bu şu demektir: Eğer B oyuncusu optimal stratejisini oynarsa, A oyuncusunun oynayacağı v değerinden daha fazla kazandırabilecek strateji yoktur.
b)  B oyuncusunun her tam strateji vektörü yt için B.D.( x*, yt) ≥v dir.

İKİ KİŞİLİ – SIFIR TOPLAMLI OYUNLAR

Bir oyunda iki oyuncu varsa oyun iki kişili oyundur. İki kişili bir oyunda oyuncuların kazançları toplamı sıfırsa oyun, iki kişili sıfır toplamlıdır. Burada;
- Biri satır oyuncusu, diğeri sütun oyuncusu olarak adlandırılan iki oyuncu vardır. Satır oyuncusu yerine bizim taraf, sütün oyuncusu yerine de karşı taraf deyimlerine rastlanabilir.
- Satır oyuncusu için m, sütün oyuncusu n tane mümkün strateji vardır. Bu oyun kısaca mxn  oyun olarak isimlendirilir.
- Satır oyuncusu stratejilerini, R1, R2, ..., Rm ile sütun oyuncusunun stratejilerini, C1, C2, ..., Cn ile gösterelim. Oyuncuların strateji seçimlerinin türlü bileşimlerinden sonuçlanan kazanç veya kayıpları bildiğimizi varsayalım. Bu tabloya, ödül, ödeme, kazanç veya kısaca “oyun matrisi” denir.

Satır oyuncusunun Ri, sütun oyuncusunun CJ  gibi belirli bir stratejiyi kabul ettiklerini varsayalım. Oyun matrisi satır oyuncusuna göre düzenlenmiş ise aij satır oyuncusunun kazancını (sütun oyuncusunun kaybını) gösterir.

Örnek 1 : Aşağıdaki kazanç matrisini dikkate alarak, oyuncuların hangi stratejilerle oynayacağını belirleyiniz.

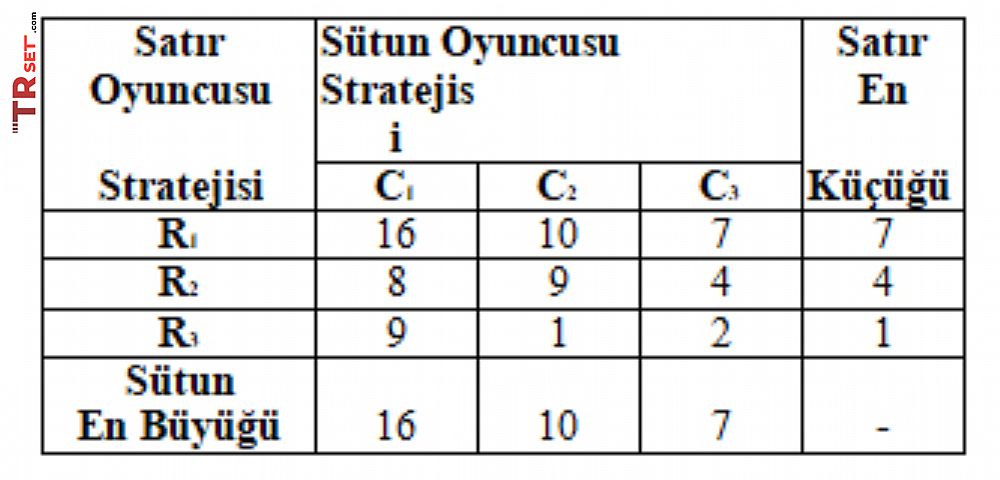
Her oyuncunun üçer stratejisi bulunduğundan oyun bir 3 x 3 oyunudur. İlk önce satır oyuncusuna bakılırsa; bu oyuncu R1 stratejisini seçerse, sütun oyuncusu C3 stratejisini seçerek kendi kaybını dolayısıyla rakibinin kazancını mümkün olan en düşük düzeyde düşer. Bu değer yukarıdaki matrise eklenen “satır en küçüğü” sütununda gösterildiği gibi 7’dir. Satır oyuncusunun ikinci stratejiyi seçmesi durumunda sütundaki oyuncu gene kendisi için en az (4) kayıp sağlayacak olan stratejiyi yani, üçüncü stratejiyi seçecektir. Sonuçta, satır oyuncusu için en iyi strateji, R1’dir.

TEPE NOKTASI KAVRAMI (TAM STRATEJİLER)

Oyunların en basiti tepe noktalı oyunudur. Yani satırında en küçük ve sütununda en büyük bir tek elamanı olan ödemeler matrisi düşünülmektedir. Bu durumda A ya göre oyunun değeri tepe noktası elemanı ve B ye göreyse tepe noktası elemanın negatif  işaretlisidir.

Örnek 2 : A ya göre ödemeler matrisi aşağıda verilmektedir. Her bir oyuncu için en iyi seçeneği, A ve B ye göre oyun değerini bulunuz.

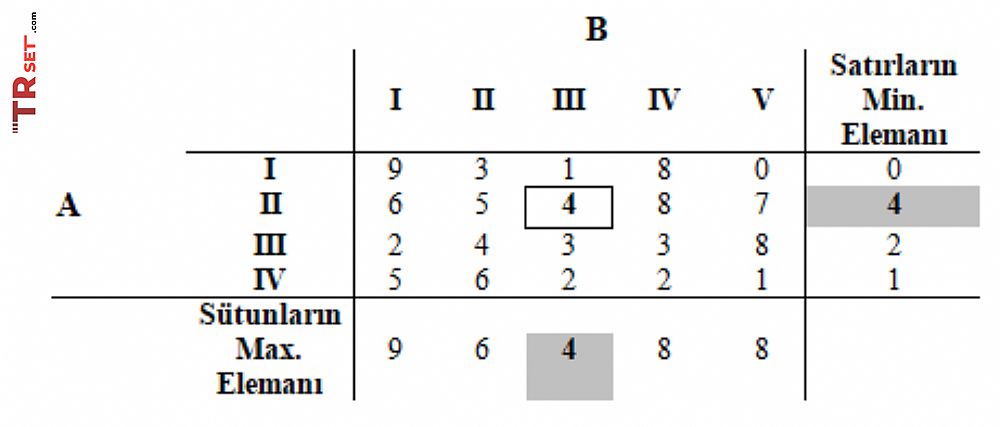
Verilen A ya göre ödemeler matrisinde her bir satırın en küçük elemanı matrisin sol tarafına ve B ye göreyse ödemeler matrisi kayıp değerleri göstermesi nedeniyle her bir sütunun en büyük elemanı matrisin altına yazılır. Bu düşünce A yönünden maximin yani kötümserlik kriteri ve B yönünden kayıp söz konusu olduğu için minimax (=maliyet tipli karar matrisinde kötümserlik kriteri) olarak belirlenir. A için oyun değeri 4 ve B için oyun değeri 4 olarak bulunması nedeniyle her iki oyuncunun oyundan beklediği değerler (birinin kazancı diğerinin kaybı olarak düşünüldüğü için) birbirini karşılamaktadır ve oyunun bir tepe noktası vardır. A nın seçeneği II. strateji, B nin seçeneği de III. stratejidir ve tam stratejileridir. Oyunun tepe noktası olması dolayısıyla da oyunun değeri 4 dür.

Makalenin Devamı
➕ Tepe Noktasız Oyunlar ve Karma Stratejiler

Kaynaklar :

-  James W. Friedman, Game Theory With Applications To Economics, 2nd ed., Oxford University Press, New York, 1990, s.3.
-  Drew Fudenberg and Jean Tirole, Game Theory, The MIT Press, Massachusetts, 1998, s. 3.
-  Osman Halaç, Kantitatif Karar Verme Teknikleri (Yöneylem Araştırması), 4.b., Alfa Basım Yayım Dağıtım, İstanbul, 1995, s. 72.
-  Ahmet Öztürk, Yöneylem Araştırması, 5.b., Ekin Kitapevi Yayınları, Bursa, 1997, s.383.
-  Nalan Cinemre, Yöneylem Araştırması, Beta Basım Yayım Dağıtım A.Ş., İstanbul, 1997, s.287.